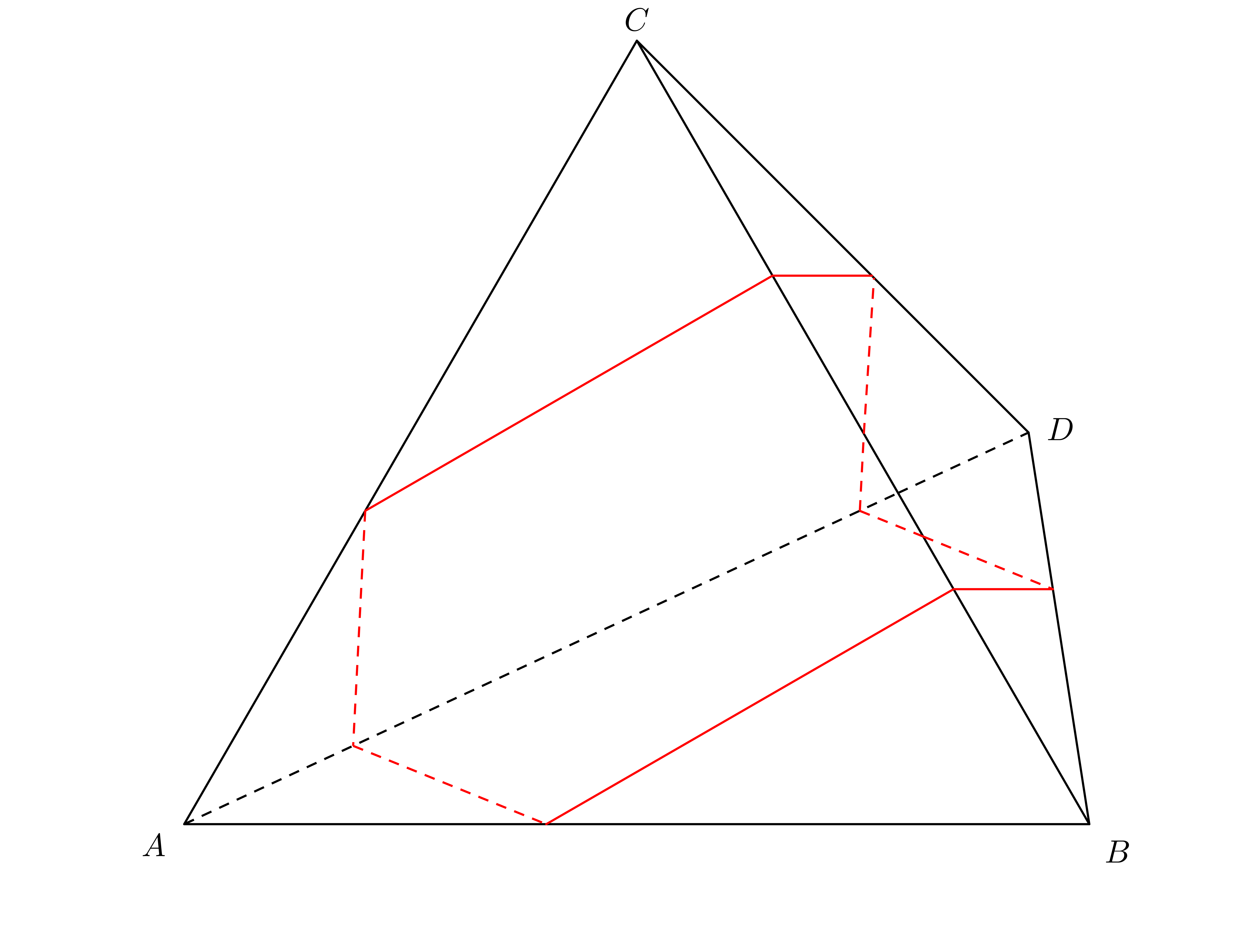
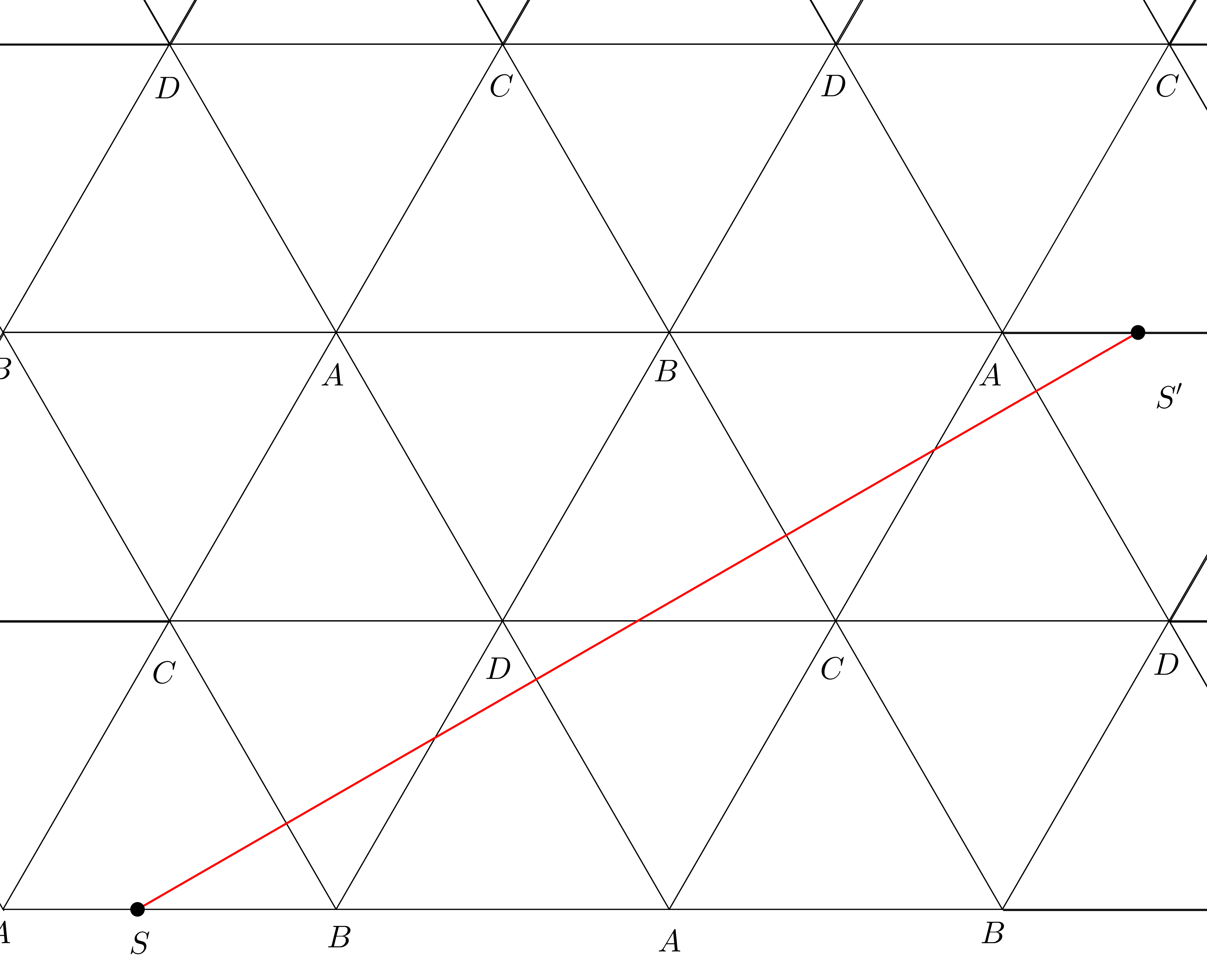
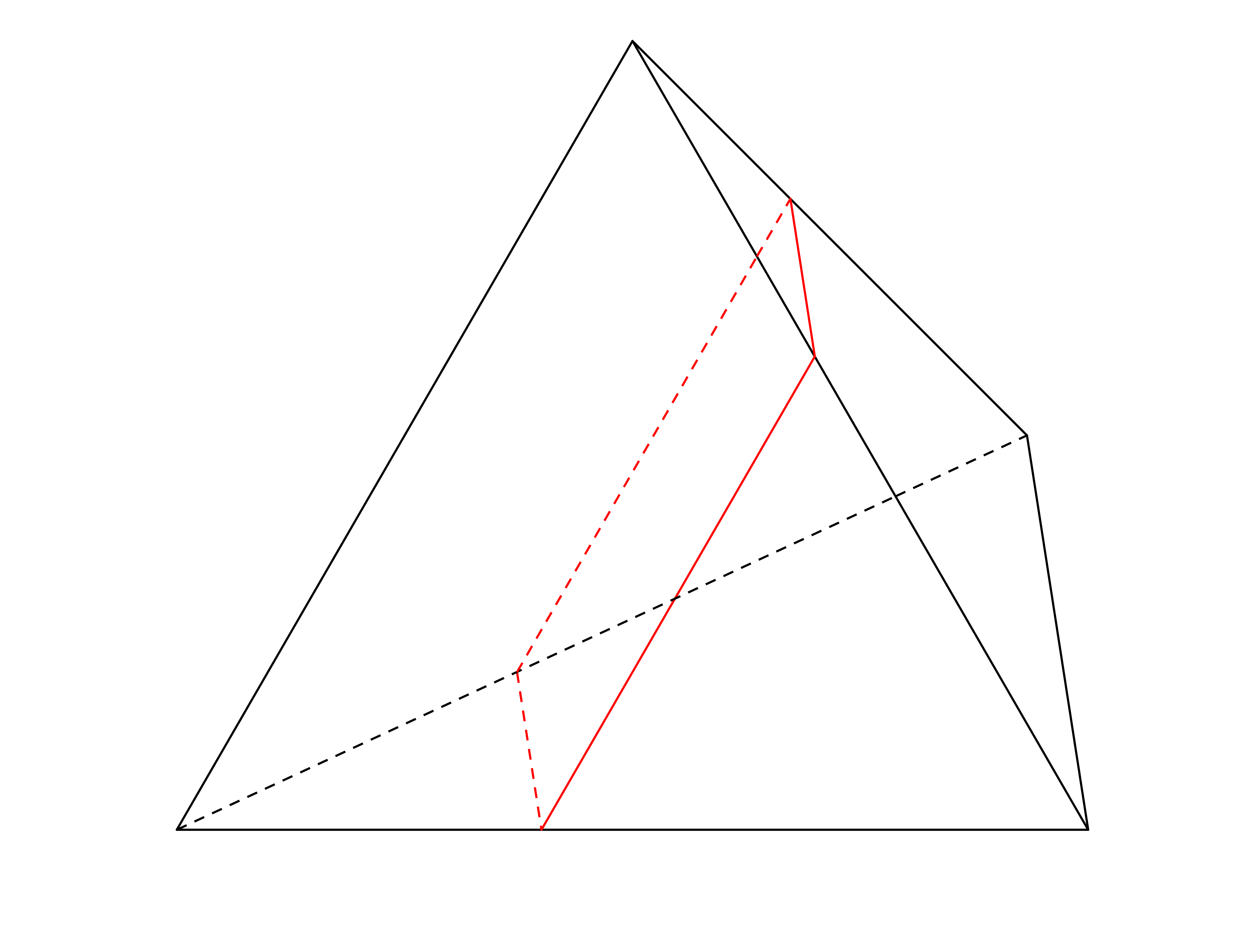
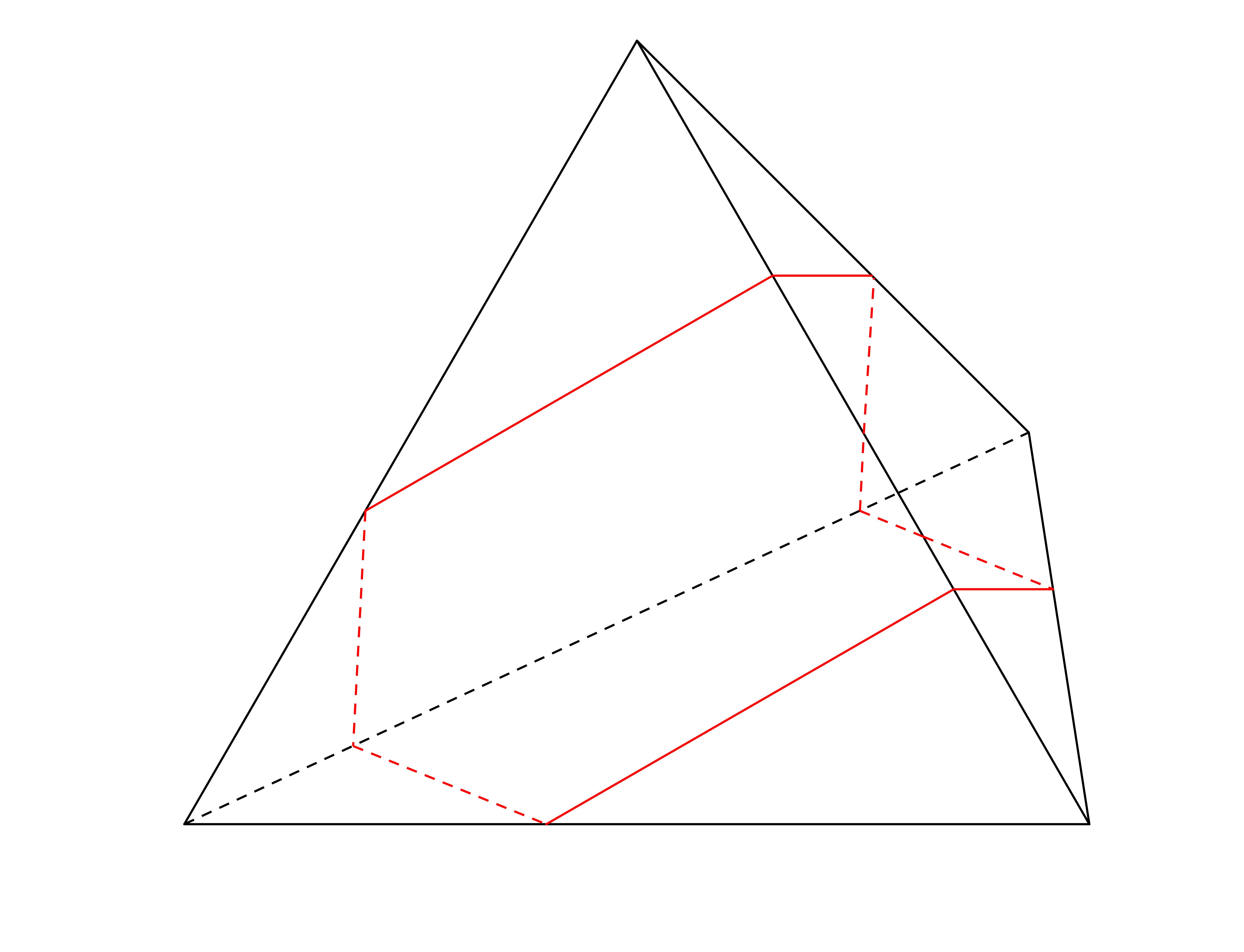
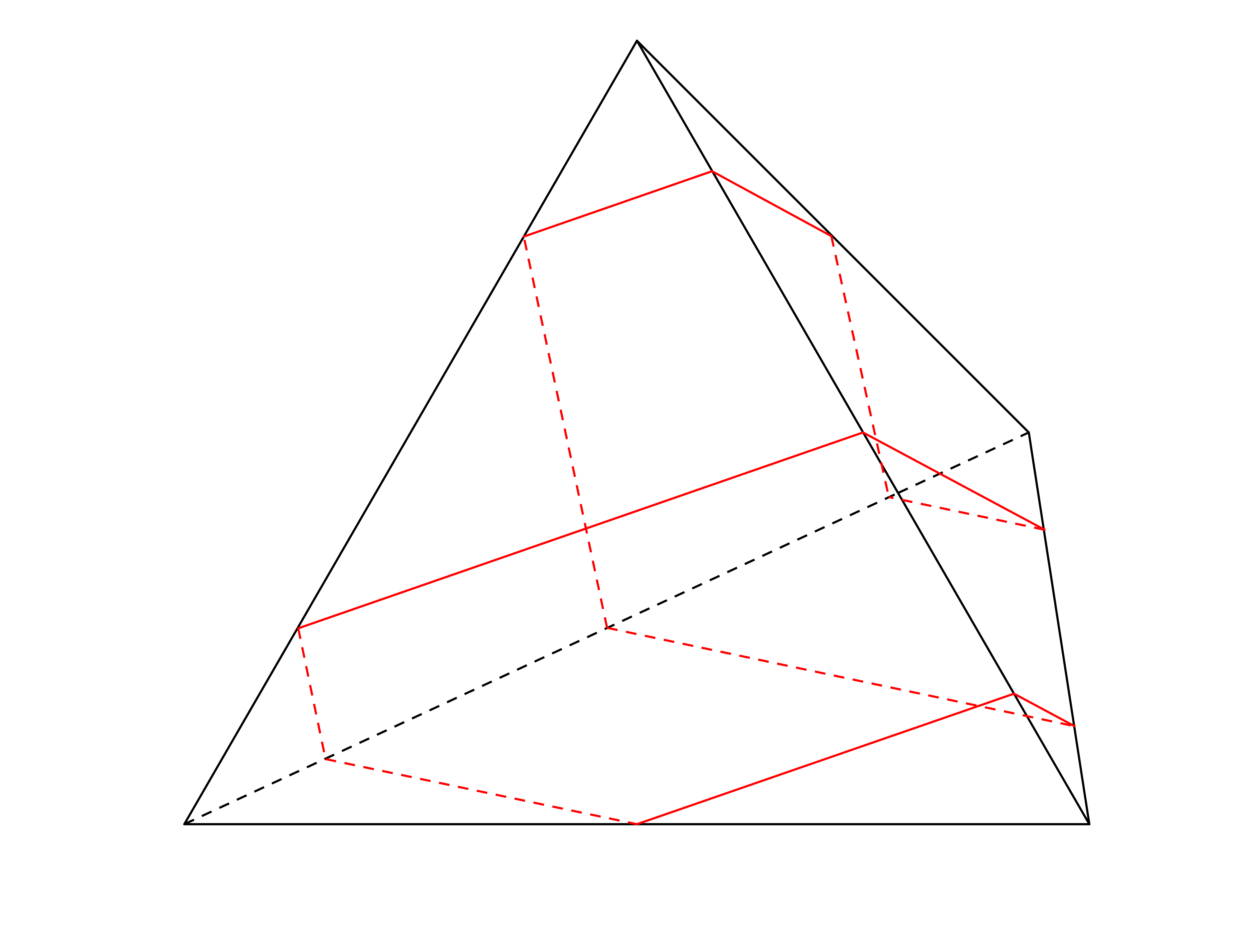
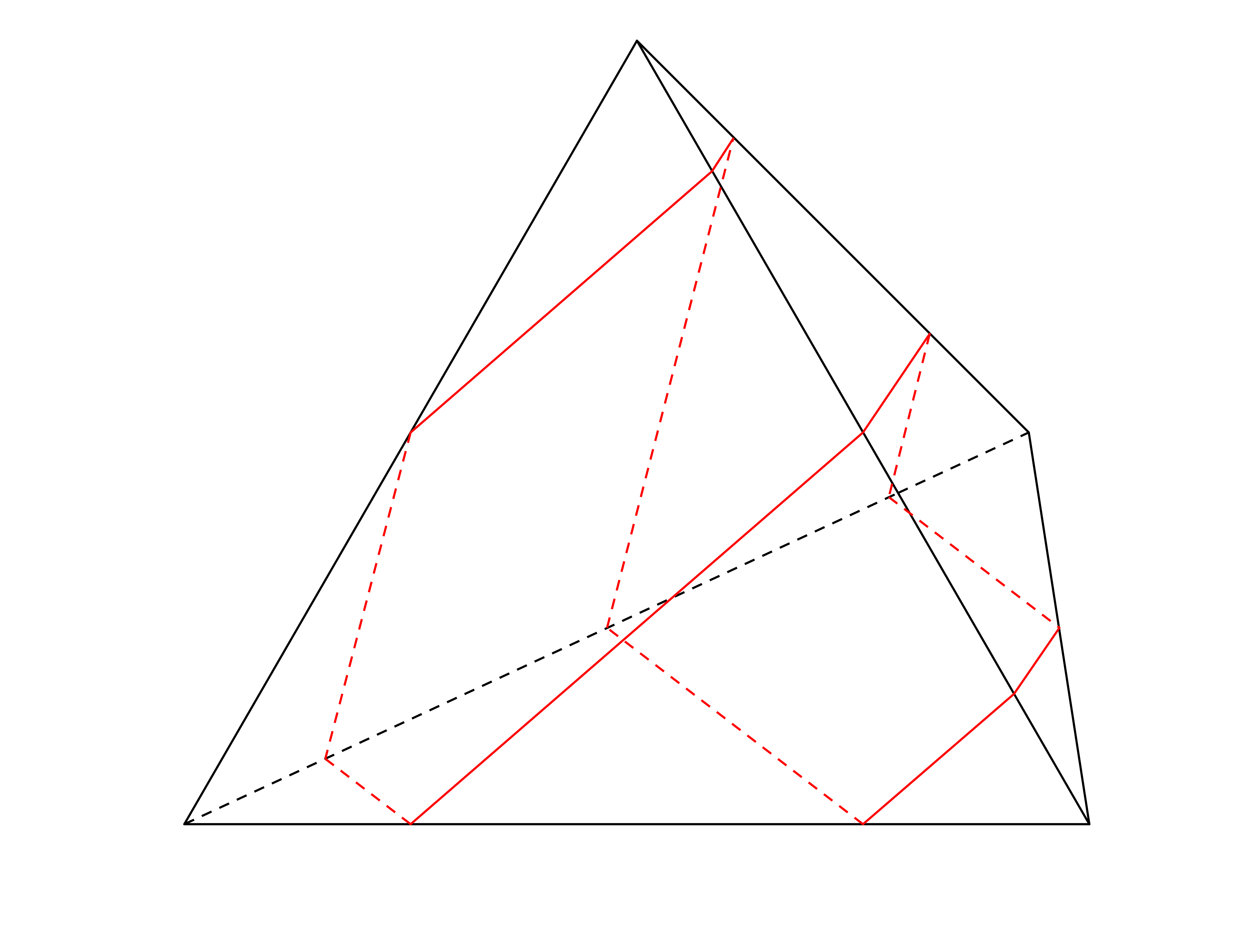
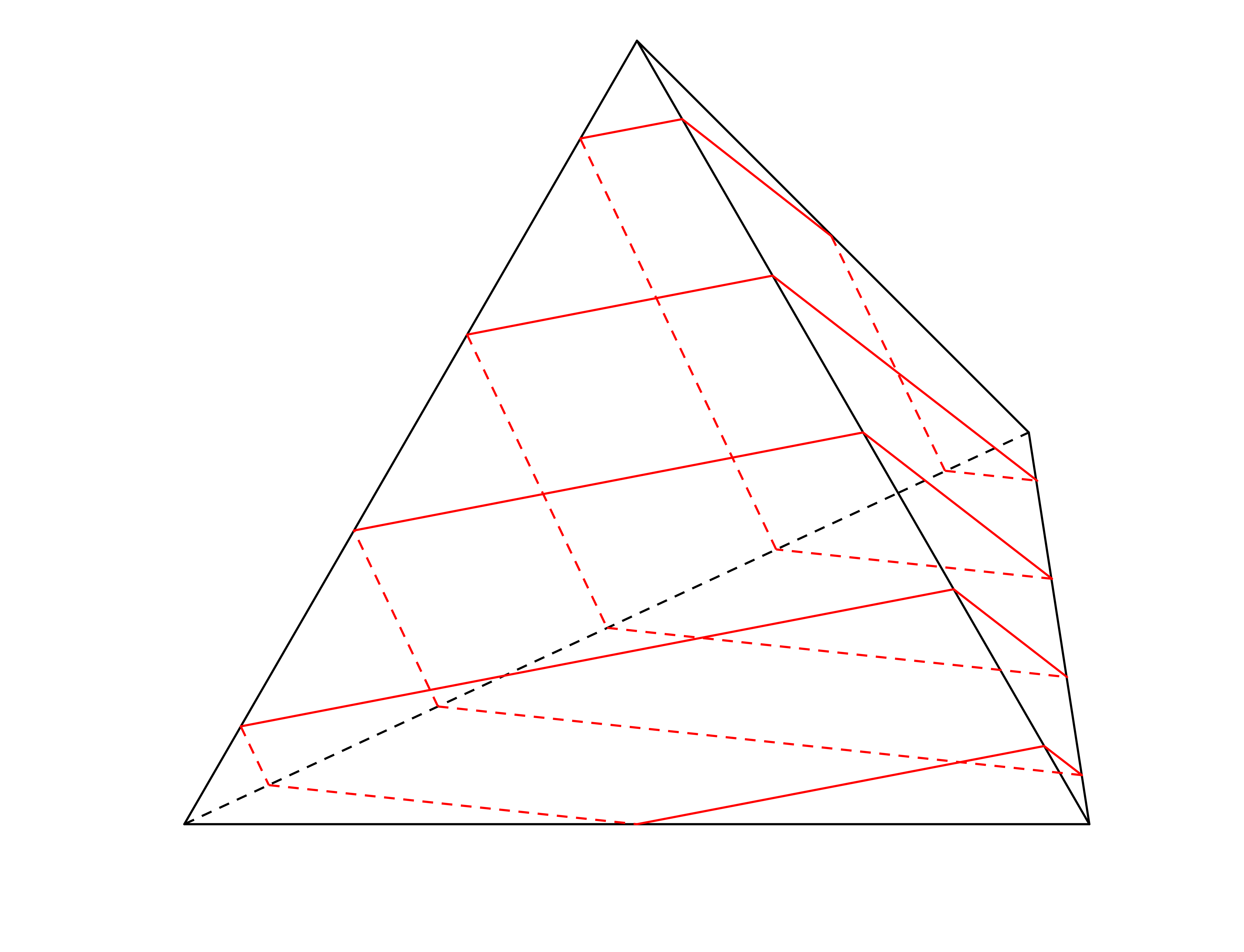
Every closed geodesic on the tetrahedron is simple, i.e. has no self intersections. This follows as on each face of the tetrahedron all the segments of a geodesic are parallel. In turn, this is implied as the regular tessellation of the plane by equilateral triangles consists only of translates of equilateral triangles and of 180-degree rotations of them. For example look at the following geodesic and its unfolding in the tesselation.This gives a pictorial proof why every closed geodesic is simple on the tetrahedron.
We next show six closed and simple closed geodesics. For a poster showing simple closed geodesics on regular polyhedra see here.